BIMI（Brand Indicators for Message Identification）について
BIMIの概要
Seth Blank氏を中心に、2019年頃からIETFで検討されているインターネットドラフトです。
メール送信者が指定するロゴをメール受信者側で表示できるようにすることで、なりすましメールでないことを視覚的に判別できるようになります。 単なるロゴ表示機能だけではなく、無関係な第三者によるロゴの使用を防ぐための仕組みも提供します。
BIMIを利用する為の前提
メールのなりすましを防ぐ既存技術、DMARCが設定済みであることが必要です。DMARCは更に別の技術、SPF と DKIM から成り立つものです。 BIMIに関係して、依存する既存技術を整理すると以下のようになります。
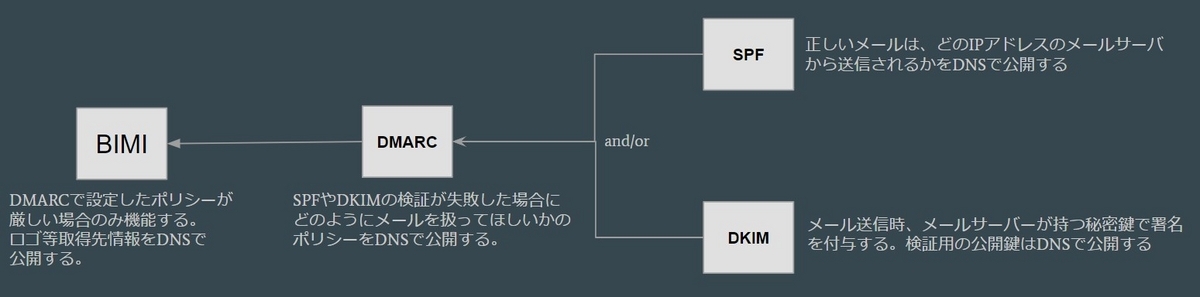
BIMIの導入により、ロゴを表示できるようになるのはもちろんですが、DMARCの普及によるメールセキュリティの改善も見込まれます。
BIMIの全体像とロゴ不正利用の防止
BIMIを用いた際のメール送受信に関する処理を以下のように図示します。 BIMIで特徴的なのは⑤の処理だと思います。メールの送信者がそのロゴを使用するにふさわしい者であることを証明する証明書が存在します。メールの受信者は、この証明書を検証することでロゴが適正に利用されていることを確認することができます。この証明書のことを、VMC（Verified Mark Certificate）といいます。
VMCの発行は、現在DigiCertとEntrustが行っているようです。この記事では、以降VMCについて深堀します。
VMCの発行について
以下の情報に対して、認証局が審査を行いお墨付きを与えたものです。
認証局にてどのような審査が行われるかについては、BIMIグループの資料を確認することで知ることができます。
https://bimigroup.org/resources/VMC_Requirements_latest.pdf
面白いところとしては、p42の3.2.16 Registered Mark Verificationにて、ロゴを認証する方法についての項目が存在するところかと思います。 申請者はしかるべきTrademark office（日本であれば、特許庁と文化庁が記載されていますね）にて商標を登録し、その商標登録番号を認証局に伝える必要があるようですね。
VMCを実際に見てみる
amazon.co.jpは、BIMIに対応しているようなので、実際に証明書の内容を見てみます。まずは、証明書がどこで公開されているかをDNSをひくことで確認します。
$ dig +short txt default._bimi.amazon.co.jp "v=BIMI1;l=https://d3frv9g52qce38.cloudfront.net/amazondefault/order_329474121_logo.svg;a=https://d3frv9g52qce38.cloudfront.net/amazondefault/amazon_web_services_inc.pem"
a=の値として記載されているURLがVMCの在り処となります。これをダウンロードして、解いてみると以下のようになります。
DigiCertが発行したVMCを用いていることが分かります。
また、OIDの1.3.6.1.5.5.7.1.12を私の環境では正しくパースできていませんが、ここにBIMIのロゴデータがSVG形式で入っているものと思われます。
Certificate:
Data:
Version: 3 (0x2)
Serial Number:
05:ba:54:0c:24:1c:f1:ff:9e:9a:77:f8:fb:82:bc:a8
Signature Algorithm: sha256WithRSAEncryption
Issuer: C = US, O = "DigiCert, Inc.", CN = DigiCert Verified Mark RSA4096 SHA256 2021 CA1
Validity
Not Before: Dec 23 00:00:00 2022 GMT
Not After : Jan 23 23:59:59 2024 GMT
Subject: jurisdictionC = US, jurisdictionST = Delaware, businessCategory = Private Organization, serialNumber = 4152954, C = US, ST = Washington, L = Seattle, street = 410 Terry Avenue N, O = "Amazon Web Services, Inc.", CN = "Amazon Web Services, Inc.", 1.3.6.1.4.1.53087.1.13 = Registered Mark, 1.3.6.1.4.1.53087.1.3 = US, 1.3.6.1.4.1.53087.1.4 = 6178564
Subject Public Key Info:
Public Key Algorithm: rsaEncryption
RSA Public-Key: (2048 bit)
Modulus:
00:c4:65:37:70:ba:65:a8:71:5a:87:7e:3e:74:80:
c8:10:5f:05:86:d5:1f:25:3d:4b:37:d8:97:f8:e7:
f5:d3:f7:6d:0b:d1:53:90:84:64:d4:37:22:ad:1f:
de:0e:0e:de:11:fc:62:42:77:8a:ff:ca:ee:16:ee:
a5:20:13:a2:d4:f5:1c:4a:e6:25:25:81:d3:c3:7f:
ff:22:c9:a6:fd:c0:77:56:e7:8c:13:e0:b8:db:36:
6c:7a:44:27:a8:39:c2:3a:f4:5b:d8:a7:9e:0c:40:
5a:23:2b:17:39:50:f3:6e:65:63:1d:3e:65:4b:18:
27:26:12:74:1a:5b:d6:77:33:ac:2f:ca:cd:8a:d0:
92:da:bd:b8:a7:37:5e:80:cc:cf:24:13:f3:7a:78:
fd:d9:f7:79:17:fc:f6:f5:cc:81:c7:c3:bb:92:f7:
f5:60:8a:f4:37:41:23:d4:a4:d8:8e:08:cd:9e:c2:
ec:e8:0f:58:4e:3f:b9:37:c5:dc:9e:cf:c9:c5:43:
1e:e5:ef:87:f0:94:3b:9e:d8:d6:7a:fb:f4:c2:7f:
d4:25:53:f5:ec:1a:f2:be:81:2a:73:a7:3b:32:ab:
e3:55:6a:f5:bc:fd:d2:9b:4d:80:8e:a7:1f:90:84:
91:43:19:44:c6:94:cf:39:e6:30:af:13:d8:54:02:
79:7b
Exponent: 65537 (0x10001)
X509v3 extensions:
X509v3 Authority Key Identifier:
keyid:BE:9F:BD:8D:57:6D:95:B5:AD:63:C3:97:4E:AB:A8:84:5D:3A:07:F5
X509v3 Subject Key Identifier:
B3:C5:40:4E:B8:57:BE:0D:44:D9:EA:BD:05:88:04:2D:87:6F:27:78
X509v3 Subject Alternative Name:
DNS:amazon.fr, DNS:amazon.it, DNS:amazon.es, DNS:amazon.eg, DNS:amazon.in, DNS:amazon.co.jp, DNS:amazon.ca, DNS:amazon.cn, DNS:amazon.com.br, DNS:amazon.com.mx, DNS:amazon.com.au, DNS:amazon.nl, DNS:amazon.ae, DNS:amazon.sa, DNS:amazon.com.tr, DNS:amazon.sg, DNS:amazon.pl, DNS:amazon.se, DNS:amazon.com, DNS:amazon.co.uk, DNS:amazon.com.be, DNS:amazon.de
X509v3 Extended Key Usage:
1.3.6.1.5.5.7.3.31
X509v3 CRL Distribution Points:
Full Name:
URI:http://crl3.digicert.com/DigiCertVerifiedMarkRSA4096SHA2562021CA1.crl
Full Name:
URI:http://crl4.digicert.com/DigiCertVerifiedMarkRSA4096SHA2562021CA1.crl
X509v3 Certificate Policies:
Policy: 2.16.840.1.114412.0.2.5
CPS: http://www.digicert.com/CPS
Policy: 1.3.6.1.4.1.53087.1.1
Authority Information Access:
CA Issuers - URI:http://cacerts.digicert.com/DigiCertVerifiedMarkRSA4096SHA2562021CA1.crt
X509v3 Basic Constraints: critical
CA:FALSE
1.3.6.1.5.5.7.1.12:
image/svg+xml0#0!0...+.........#.J.9.....$y.I.|...0......~data:image/svg+xml;base64,H4sIAAAAAAAACl1STY+bMBC976+wvFd78Iw/sKuQVbZSb5UqtXvpjRKSILEQBRR2++s7Jm2VVpZnMON5b96DzdPbay+u7WXqxqGSCEaKdmjGfTccK/ny7ZOOUkxzPezrfhzaSr63k3zaPmym6/G+jaT4UU/tl8t46Hq+NnfDuz5PUly7dnke3ypphBGYKG8pmHSYKnma5/OHoliWBRYL4+VYkDGmYGy5fRBiM3dz3253r/XPcdgUt1N+f2mbWTR9PTFG008apWDavpKPh8NBiqXbzyeeKjOd2u54mm+HYm0+1/Ppvpn+NpOlg22l2FfyM3oH3qnkwIaPaCM4hSYAlQrR8yYIuRh/P+/QRDBcvCXDCxUhJKeigzI1GsEjB1tqwKAtkFUIIWgCjDt0AQIz3JJZVwrgGd0Qv/Zg4p90q6InIJUM+NgQlMTQPBffh6gIrFMWyvj9XvJ/Iv91YJUc+DsGFXkGnpdYB4fgNdo1AnGIrFhDsFlOBEyc48qdNLisJakE5HQAlxSxeVE7CGxFAMx1575iKCFElRiKVaRsa3bHZj+QMiV4ThpVto/bY6kCMKOHMiiX0XkMt2rb5H9l+wsPfa8QxQIAAA==
CT Precertificate SCTs:
Signed Certificate Timestamp:
Version : v1 (0x0)
Log ID : 55:59:53:AE:30:96:00:80:6C:D2:EB:52:08:A6:C9:9E:
93:18:28:AC:10:56:B4:42:1C:55:36:15:4C:5F:75:AC
Timestamp : Dec 23 21:16:05.891 2022 GMT
Extensions: none
Signature : ecdsa-with-SHA256
30:45:02:21:00:B6:DF:61:82:C8:48:A7:03:E3:7A:CC:
82:38:D0:38:A7:99:74:45:A4:FB:32:EA:0F:90:A6:FD:
BC:C0:EE:67:52:02:20:31:86:87:F6:5C:31:16:EA:90:
D1:5F:A3:13:70:D9:25:E6:39:C1:04:D4:39:F9:4B:B7:
AD:73:6F:E6:D2:F1:CE
Signature Algorithm: sha256WithRSAEncryption
66:a4:1c:c8:d3:d7:e8:61:18:e3:43:7f:5c:4b:8e:43:56:18:
8b:83:bd:a9:50:e8:1e:d1:0c:8c:96:bf:f0:be:94:b5:25:90:
a1:56:e6:c6:47:ae:9b:eb:52:14:4a:f5:39:d5:4a:59:b3:e3:
5e:a5:65:50:5e:35:d4:90:e0:07:ea:04:2d:8d:d3:7a:eb:1d:
ad:ad:71:09:df:c1:ef:89:6a:bb:1f:13:2f:b2:d6:5e:36:c2:
34:3a:42:f3:30:c2:7b:95:f6:cc:ac:77:91:1e:c9:91:3a:91:
38:df:b9:9d:a0:d7:3d:ef:69:ba:30:c2:91:8a:e4:62:18:92:
20:d3:39:8e:2c:62:ca:c0:74:bf:57:30:89:e8:f3:db:77:1f:
9c:eb:e9:b0:6d:7a:5c:47:0c:1e:bc:15:43:65:4b:dd:64:d6:
1a:4c:98:f8:2f:2f:14:24:8b:0b:25:1e:58:d9:c8:16:23:2d:
45:97:7c:8e:6d:4c:7c:c4:2e:9b:5a:8e:58:57:49:99:05:b6:
3c:6c:fa:05:f8:e5:8a:d0:49:10:35:78:17:c2:7e:e0:fd:0b:
94:cf:4d:90:a3:a4:0d:77:cb:a1:54:32:c7:b4:7b:af:2d:db:
9b:4d:f0:51:18:ab:42:87:fc:4d:60:d0:c2:85:22:b5:31:0b:
90:78:c0:6b:17:f8:98:37:a1:fa:bd:14:16:1f:d2:ee:5d:a8:
6b:a2:22:73:13:1b:1f:0b:9b:0c:4c:2d:5f:f4:7e:e1:28:9b:
68:ad:1a:c9:a0:45:65:81:c9:80:04:a6:3b:7b:8e:26:9b:dd:
76:5c:31:76:df:b7:50:b1:9a:ea:3a:38:77:cd:61:61:e4:e6:
66:73:e2:d8:9a:c6:46:97:8d:0e:00:c0:e2:a7:9c:51:de:d3:
4b:51:d0:6e:aa:e1:3d:9d:94:8d:fb:5c:f4:d6:78:8a:84:dd:
f2:e1:aa:f6:1f:2f:77:fc:e6:68:2e:79:68:e8:31:aa:79:ea:
1e:6b:c1:ec:c6:16:48:ed:d8:ce:40:95:96:45:da:fa:ab:30:
58:91:d7:f7:08:ad:31:0e:d4:37:91:35:3c:71:fd:9c:5a:c2:
1d:ae:b8:b5:46:6a:6c:e4:11:5c:fd:9d:74:26:ca:7e:44:c8:
a2:88:70:ab:e5:7f:5c:a5:29:66:02:e6:fb:f3:7d:1b:e2:75:
7e:34:f2:a7:bb:a8:30:bc:46:ff:f9:13:41:39:8a:f8:28:fa:
11:66:1c:d0:4b:10:a7:b9:7a:66:99:57:b7:e1:29:ef:a5:24:
4e:15:60:06:38:ed:c6:7b:44:02:54:58:60:d6:69:0e:cb:0c:
b9:08:8c:a9:84:f4:58:63
VMCはどれくらい発行されているか
2023/02/25時点の情報を、Certificate Transparencyの仕組みを用いて調べてみました。
国別発行件数
| 国 | 件数 |
|---|---|
| アメリカ | 1,805件 |
| イギリス | 553件 |
| ドイツ | 241件 |
| オーストラリア | 164件 |
| インド | 162件 |
| 日本 | 127件 |
その他の国含めた発行割合は以下の通りでした。
ちなみに日本の127件のうち、具体的な組織としては以下のようなところがありました。 Paidy, Inc.、Rakuten Group, Inc、株式会社ビューカード、SmartHR, Inc.、QUALITIA CO., LTD、
これから普及していってほしいですね。
なお、CTのログサーバーについては、先ほどのBIMIグループの資料のp.90のAPPENDIX F - CT LOGS APPROVED BY AUTHINDICATORS WORKING GROUPに記載があります。
現在では、DigiCertが運用するGorgonというもの1つだけのようですので、このログサーバーを調べました。
TLSAレコードでTrust Anchor Assertionを設定する
概要
- 私の管理するドメイン名、mtcq.jpにTLSAレコードを設定してみました。
- その時に調べたことなどをメモしておきます。
TLSAレコードでできること
TLSAレコードを設定することで、ドメイン名とサーバー証明書（以下、エンドエンティティ証明書）に関する情報をDNSで紐づけすることができます。
TLSクライアントが対象ドメイン名に対してTLS通信を試行する際に、この紐づけ情報をチェックすることができるようになります。 *1
紐づける方法（以下、Certificate Usage）は、4つが存在します。
| Certificate Usage | ドメイン名に紐づけする情報 |
|---|---|
| 0 | 対象ドメイン名に対してエンドエンティティ証明書を発行した認証局の情報 |
| 1 | 対象ドメイン名に対して発行されたエンドエンティティ証明書の情報 |
| 2 | 対象ドメイン名に対して発行されたエンドエンティティ証明書のルート証明書の情報 |
| 3 | 対象ドメイン名に対して発行されたエンドエンティティ証明書の情報(上述の1と異なり、自己署名証明書でよい) |
なぜTLSAレコードが作られたか
エンドエンティティ証明書を発行する認証局が過去に起こした事故が関係しています。
現在ウェブで用いられているエンドエンティティ証明書は、技術的にはどの認証局がどのドメイン名に対しても発行することができます。
例えば、example.comの管理者はいつも認証局Aから証明書を発行していたとします。悪意のある第三者が何らかの方法でexample.comの証明書を
認証局B（システムが脆弱でクラックされてしまったなど）から得たとします。この場合、認証局Bから得た証明書も問題なく使えてしまうという課題があります。*2 *3
具体的な事故事例としては、オランダの認証局DigiNotarが過去に起こした事故などがあります。
TLSAレコードが存在することにより、あるドメインで使用されるべき本物の証明書がどれであるのかを明確にすることができますので、このような問題の発生を低減することができます。
なお、TLSAレコードはその性質上DNSSECが有効化されていることが必須となります。*4
CAAレコードとの違い
ドメインの管理者はCAAレコードを設定することで、自身のドメインに証明書を発行してもよい認証局を指定することができます。認証局は、証明書を発行するタイミングでCAAレコードを引き、もし自身を指定する情報が記載されていなかった場合は証明書を発行しない挙動をとります。 *5
CAAレコードが証明書を発行するタイミングで働くの対し、TLSAレコードはTLSの証明書チェーン検証のタイミングで働く違いがあります。
設定した内容
Let's Encryptのエンドエンティティ証明書を設定している私のドメイン mtcq.jp について、以下のTLSAレコードを設定してみました。 Certificate Usageは2番で、ルート証明書に対するアサーションを入れるものとなります。
$ dig +short _443._tcp.mtcq.jp. -t TLSA 2 1 1 0B9FA5A59EED715C26C1020C711B4F6EC42D58B0015E14337A39DAD3 01C5AFC3
なお、Shumon Huque氏が作った以下のツールを用いることで、TLSAレコードの内容を簡単に作ることができます。
ただ念のため、レコードの内容が正しいかどうかチェックしてみます。 今回私は以下の設定でレコードを作成しています。
| Certificate Usage | Selector | Matching Type |
|---|---|---|
| 2 | 1（証明書のSubjectPublicKeyInfo部分の情報を用いる） | 1（sha-256ハッシュで表す） |
Let's Encrtyptのルート証明書のPEMを取得し、SubjectPublicKeyInfoの情報を保存します。 (241バイトからSubjectPublicKeyInfoの情報が始まっています)
抜き出した情報のsha-256をとればよいです。
$ openssl asn1parse -strparse 241 -in ISRG-ROOT-X1 -noout -out spki.der $ sha256sum spki1.der 0b9fa5a59eed715c26c1020c711b4f6ec42d58b0015e14337a39dad301c5afc3
レコードは正しく作れていそうです。
TLSAレコードの面白いところ
今回試せていませんが、Certificate Usageの3がとても面白いと思いました。
これを用いれば、TLSAレコードで自己署名証明書を提供することができます。TLSAレコードは、DNSSECで署名されることが期待されますので、認証局のような余分なTTPを必要とせずに信頼の連鎖を構築することができます。別の機会に設定してみて、対応しているクライアントを探すなどしてみたいと思います。
TLSAレコードの課題
個人的に感じる課題についてです。
- TLSAレコードをチェックするTLSクライアントがほとんど存在しない？
- DNSSECが普及していない
CRLiteの仕組み：Bloom filterの偽陽性をなくす方法
はじめに
TLS証明書の失効情報を管理する新たな仕組みとして、CRLiteというものが考えられています。（以下の論文です）
CRLiteの根幹部分は、偽陽性を排したBloom filterで成り立っています。
この記事では、どのようにしてそのような偽陽性のないBloom filterを作るのか記載します。
まずは、Bloom Filterについて説明します。
Bloom filterについて
概要
Bloom filter（以下、BF）自体は1970年に考案されたデータ構造なだけあり、既に様々なウェブサイトにて解説がなされています。 このデータ構造の典型的な使い道の一つとして、ブラックリストがあります。あるデータが、許容されないリスト（ブラックリスト）に記載されているか否かを判別したいとき、これを用いることで高速に（どんなにブラックリストが大きくなっても定数時間で）判別を行うことができます。
但し、素のBFにはデメリットとして偽陽性（False Positive）があります。
偽陽性：本当はリストに含まれて いない データなのに、含まれて いる と判別してしまう。
なお、偽陰性はありません。
偽陰性：本当はリストに含まれて いる データなの、含まれて いない と判別してしまう。
言い換えると、「含まれている！」という判定をBFから得た時は、誤りである可能性があります*1が、「含まれていない！」という判定を得た時は、確実に正しいということです。
仕組み
適当なサイズの配列と、適当な個数のハッシュ関数*2を用意することでBFを構築することができます。たとえば、配列長8、ハッシュ関数2個（md4とmd5とします）の場合を考えます。
データの追加
appleという文字列を追加することにします。追加するデータに対して、先のハッシュ関数でハッシュ値を求めます。ハッシュ値（整数）は、配列のインデックスの為に使用します。ただ、ハッシュ値そのままでは長大ですから、配列長に収まる数となるように配列の長さで割った余りを求めます。
| データ | ハッシュアルゴリズム | hash値 | hash値を8で割った余り（インデックス） |
|---|---|---|---|
| apple | md4 | 0x9443a56f029a293d8feff3c68d14b372 | 2 |
| apple | md5 | 0x1f3870be274f6c49b3e31a0c6728957f | 7 |
求めたインデックスが指し示す配列の値を、1にしておきます。BFではこれでデータを追加したこととなります。
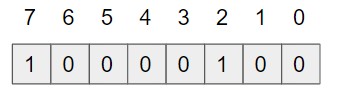
データの存在確認
先のBFに、データorangeが存在しているか確認してみます。まず、同様にハッシュ値を求めます。
| データ | ハッシュアルゴリズム | hash値 | hash値を8で割った余り |
|---|---|---|---|
| orange | md4 | 0xb0e795cd4b8b3c8247a09cbcd6f4a76c | 4 |
| orange | md5 | 0xfe01d67a002dfa0f3ac084298142eccd | 5 |
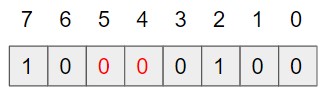
求めたインデックスを用いて配列の値を確認し、全てが1である場合はデータが存在するということとなります。
そうでない場合、１つでも0の箇所があるなら、データorangeは存在しないこととなります。
今回の場合、配列[4]と配列[5]の値はどちらも0なので、orangeは存在しないこととなります。
性質
先の例のように、データを追加する時も検索するときも、必要なのは固定回数のハッシュ値の計算と配列参照だけです。そのため、どんなにデータが増えても処理時間に問題が生じることはありません。また、データの追加に伴って配列が長くなることもありません。これは、BFのメリットです。
一方で、orange以外のデータで偶然配列の番号が4,5となるようなものがあったとします。そうすると、誤ってBFにデータが含まれていると判断する原因になります。これは、データが追加され配列の中が埋まっていくほど発生しやすくなります。これは、BFのデメリットです。
改善
なお、配列長や用意するハッシュ関数の個数を調整することで、BFの偽陽性を減らすことはできます。ただし0にすることはできません。
BFで管理したいデータの見込み数や、偽陽性の確率を入力すると適切な配列長やハッシュ関数の数を計算してくれるサイトがありますので、こちらを参考にすると良さそうです。
Filter Cascade Design
BFの偽陽性なくす方法について説明します。
残念ながらいつでも偽陽性をなくすことができる、というわけではありません。
BFを作成する時点で、BFに追加するデータと 追加しないデータ の全て（これを、 $ U $ とします）が分かっている場合、BFを多段に構築（カスケード）することで偽陽性をなくすことができます。
ここでは追加するデータの集合を $A$ とし、追加しないデータの集合を $B$ とします。 $ A \cup B = U, A \cap B = \varnothing $ であるとして、構築手順の例を説明します。
データの追加
- $ A $を用いて通常通り、素のBFを構築します。これを、$ BF_1 $ とします。
- $ BF_1 $ が判断を誤ってしまうデータを見つけ（そのようなデータは、 $B$の要素として存在することとなります）、これを $ FP_1 $ とします。
- もし、$ FP_1 = \varnothing $ であるなら、偽陽性のないBFの完成です（1段）。そうでないなら、次の手順を続けます。
- $ FP_1 $を用いてBFを構築します。これを、$ BF_2 $ とします。
- $ BF_2 $ が判断を誤ってしまうデータを見つけ（そのようなデータは、 $A$の要素として存在することとなります）、これを $ FP_2 $ とします。
- もし、$ FP_2 = \varnothing $ であるなら、偽陽性のないBFの完成です（2段）。そうでないなら、次の手順を続けます。
- $ FP_2 $を用いてBFを構築します。これを、$ BF_3 $ とします。
- $ BF_3 $ が判断を誤ってしまうデータを見つけ（そのようなデータは、 $FP_1$の要素として存在することとなります）、これを $ FP_3 $ とします。
- もし、$ FP_3 = \varnothing $ であるなら、偽陽性のないBFの完成です（3段）。そうでないなら、次の手順を続けます。 （以下、省略）
このようにして、多段のBFを作成します。この例では、$ FP_3 = \varnothing $であったとして3段のBFを作成したものとします。
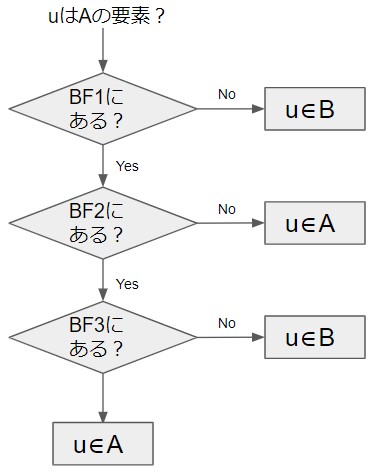
データの存在確認
上記で作成した多段のBFに順々に問い合わせを行うことで、確認します。
Web Key DirectoryでPGPの公開鍵を配布する
概要
次のインターネットドラフト（以下、I-D）に基づいて、PGPの公開鍵を配布してみたので、そのメモを残します。
WKDとは
Web Key Directoryの略で、PGPの公開鍵をHTTPSで公開する仕組みです。 PGPの公開鍵を公開する方法はすでに他のものが様々ありますが、それらがもつ課題の解決を目指しているようです。I-Dには、以下のようなことが記載されていました。
| 既存の方法 | 課題 |
|---|---|
| DNSで配布する方法 | 必ずしもメールプロバイダがDNSの管理をしているわけではない |
| 始めのメールに公開鍵を添付する方法 | 始めのメールが改ざんされる可能性がある |
| 鍵配布サーバーを用いる方法 | メールアドレスと鍵の対応性が正しく管理できない場合がある |
公開用のURL
公開用のURLは、directとadvancedと呼ばれる2つの形式があるようですが、いずれかのURLでバイナリ形式の公開鍵を公開すればよいです。I-Dに倣い、メールアドレスがJoe.Doe@example.orgである場合のURLの例を以下に記載します。
direct method
https://example.org/.well-known/openpgpkey/hu/iy9q119eutrkn8s1mk4r39qejnbu3n5q?l=Joe.Doe
無作為に見える文字列、iy9q119eutrkn8s1mk4r39qejnbu3n5qは、メールアドレスのローカルパートであるJoe.Doeを変換することで作る文字列となります。
変換の方式ですが、以下で行うことができます。
- 小文字にする（Joe.Doe → joe.doe）
- sha1でハッシュをとる（joe.doe → a83ee94be89c48a11ed25ab44cfdc848833c8b6e）
- ハッシュした値(バイナリ)を、Z-Base32でエンコードする（a83ee94be89c48a11ed25ab44cfdc848833c8b6e → iy9q119eutrkn8s1mk4r39qejnbu3n5q）
advanced method
direct methodとほとんど一緒ですが、openpgpkeyというサブドメインをつくる必要が生じます。
https://openpgpkey.example.org/.well-known/openpgpkey/example.org/hu/iy9q119eutrkn8s1mk4r39qejnbu3n5q?l=Joe.Doe
公開の仕方
I-Dでは、上記のURLに公開鍵を配置するまでの仕組みが、Web Key Directory Update Protocolとして記載されています。
draft-koch-openpgp-webkey-service-14
ただ、お手軽に試すには少々時間が掛かりそうな内容ですので、手動で公開することにしました。 まずは、公開するためのPGPの鍵ペアをThunderbirdで作り、適当なファイルにエクスポートします。
エクスポートしたファイルの中には、-----BEGIN PGP PUBLIC KEY BLOCK-----と-----END PGP PUBLIC KEY BLOCK-----で囲まれたデータが記載されています。
このデータの形式はASCII Armoredであり、以下で述べられている通りバイナリに変換する必要があります。
The HTTP GET method MUST return the binary representation of the OpenPGP key for the given mail address.
フッターとヘッダーを取り除き、そのまま変換したくなりますが、データの末尾にはCRCを示す情報が付加されているのでそれを削除してからbase64 -dなどでバイナリにします。
そのファイルをサーバーにアップロードすればよいです。
正しく公開できたか確認する
こちらのツールを利用することで、正しい形式の鍵が公開できているか確認することができました。
メールソフトで利用する
このあたりに記載されているメールソフトを利用することで、WKDで公開鍵を取得し検証等に利用してくれるはずですが、確認はできていません。
https://wiki.gnupg.org/WKD#Implementations
ThunderbirdはEnigmailなどのアドオンを用いることなく内蔵の機能でpgpメールを送れるようにりましたが、WKDについてはまだアドオン使わないといけない感じでしょうかね。
Chromeの履歴はSQLiteらしいのでいじってみる
概要
- Chromeの履歴はSQLiteで管理されているらしく、容易に中身を見れそうなので試してみました。
- 自分のChromeの履歴を用いて、どのウェブサイトに頻繁にアクセス（回数、滞在時間）しているか見てみます。
おことわり
- SQLiteの.schemaコマンドを用いることで、どのようなテーブルが定義されているかは分かりますが、その使われ方（どのようなイベントが起きた時に、レコードが積まれるのか・レコードが更新されるのか）について明確に説明している公式情報を見つけられませんでした。
- そのため、今回実行したSQLが目的の情報を正しく取得するものとなっているかは微妙なところがあります。
テーブル定義を見てみる
Historyファイル*1をsqlite3コマンドがある環境にコピーして開きます。.schemaコマンドで、定義されているテーブルを確認すると
以下、17のテーブルが定義されていました。
urls、visits、keyword_search_termsあたりに面白そうなデータが入っていそうです。
CREATE TABLE meta(
key LONGVARCHAR NOT NULL UNIQUE PRIMARY KEY,
value LONGVARCHAR);
CREATE TABLE downloads (
id INTEGER PRIMARY KEY,
guid VARCHAR NOT NULL,
current_path LONGVARCHAR NOT NULL,
target_path LONGVARCHAR NOT NULL,
start_time INTEGER NOT NULL,
received_bytes INTEGER NOT NULL,
total_bytes INTEGER NOT NULL,
state INTEGER NOT NULL,
danger_type INTEGER NOT NULL,
interrupt_reason INTEGER NOT NULL,
hash BLOB NOT NULL,
end_time INTEGER NOT NULL,
opened INTEGER NOT NULL,
last_access_time INTEGER NOT NULL,
transient INTEGER NOT NULL,
referrer VARCHAR NOT NULL,
site_url VARCHAR NOT NULL,
tab_url VARCHAR NOT NULL,
tab_referrer_url VARCHAR NOT NULL,
http_method VARCHAR NOT NULL,
by_ext_id VARCHAR NOT NULL,
by_ext_name VARCHAR NOT NULL,
etag VARCHAR NOT NULL,
last_modified VARCHAR NOT NULL,
mime_type VARCHAR(
255) NOT NULL,
original_mime_type VARCHAR(
255) NOT NULL,
embedder_download_data VARCHAR NOT NULL DEFAULT '');
CREATE TABLE downloads_url_chains (
id INTEGER NOT NULL,
chain_index INTEGER NOT NULL,
url LONGVARCHAR NOT NULL,
PRIMARY KEY (id, chain_index) );
CREATE TABLE downloads_slices (
download_id INTEGER NOT NULL,
offset INTEGER NOT NULL,
received_bytes INTEGER NOT NULL,
finished INTEGER NOT NULL DEFAULT 0,
PRIMARY KEY (download_id, offset) );
CREATE TABLE typed_url_sync_metadata (
storage_key INTEGER PRIMARY KEY NOT NULL,
value BLOB);
CREATE TABLE IF NOT EXISTS "urls"(
id INTEGER PRIMARY KEY AUTOINCREMENT,
url LONGVARCHAR,
title LONGVARCHAR,
visit_count INTEGER DEFAULT 0 NOT NULL,
typed_count INTEGER DEFAULT 0 NOT NULL,
last_visit_time INTEGER NOT NULL,
hidden INTEGER DEFAULT 0 NOT NULL);
CREATE TABLE sqlite_sequence(
name,
seq);
CREATE TABLE visit_source(
id INTEGER PRIMARY KEY,
source INTEGER NOT NULL);
CREATE TABLE keyword_search_terms (
keyword_id INTEGER NOT NULL,
url_id INTEGER NOT NULL,
term LONGVARCHAR NOT NULL,
normalized_term LONGVARCHAR NOT NULL);
CREATE TABLE segments (
id INTEGER PRIMARY KEY,
name VARCHAR,
url_id INTEGER NON NULL);
CREATE TABLE segment_usage (
id INTEGER PRIMARY KEY,
segment_id INTEGER NOT NULL,
time_slot INTEGER NOT NULL,
visit_count INTEGER DEFAULT 0 NOT NULL);
CREATE TABLE content_annotations (
visit_id INTEGER PRIMARY KEY,
floc_protected_score DECIMAL(
3,
2),
categories VARCHAR,
page_topics_model_version INTEGER,
annotation_flags INTEGER DEFAULT 0 NOT NULL,
entities VARCHAR,
related_searches VARCHAR,
visibility_score NUMERIC DEFAULT -1,
search_normalized_url,
search_terms LONGVARCHAR,
alternative_title);
CREATE TABLE context_annotations(
visit_id INTEGER PRIMARY KEY,
context_annotation_flags INTEGER DEFAULT 0 NOT NULL,
duration_since_last_visit INTEGER,
page_end_reason INTEGER,
total_foreground_duration NUMERIC DEFAULT -1000000);
CREATE TABLE clusters(
cluster_id INTEGER PRIMARY KEY,
score NUMERIC NOT NULL);
CREATE TABLE clusters_and_visits(
cluster_id INTEGER NOT NULL,
visit_id INTEGER NOT NULL,
score NUMERIC NOT NULL,
PRIMARY KEY(cluster_id, visit_id))WITHOUT ROWID;
CREATE TABLE downloads_reroute_info (
download_id INTEGER NOT NULL,
reroute_info_serialized VARCHAR NOT NULL,
PRIMARY KEY (download_id) );
CREATE TABLE IF NOT EXISTS "visits"(
id INTEGER PRIMARY KEY AUTOINCREMENT,
url INTEGER NOT NULL,
visit_time INTEGER NOT NULL,
from_visit INTEGER,
transition INTEGER DEFAULT 0 NOT NULL,
segment_id INTEGER,
visit_duration INTEGER DEFAULT 0 NOT NULL,
incremented_omnibox_typed_score BOOLEAN DEFAULT FALSE NOT NULL,
opener_visit INTEGER,
originator_cache_guid TEXT,
originator_visit_id INTEGER);
集計してみる
どれくらい頻繁にウェブサイトにアクセスしているか確認したいので、urls、visitsのテーブルを用いれば良さそうです。
ドメイン単位に、どれくらいの時間閲覧していたか、どれくらいの回数アクセスしたかを集計するSQLを書いてみます。
閲覧時間について
閲覧時間が長いドメイン順にソートして、上位5件を取得しました。
sqlite> WITH joined_http_url AS (
...> SELECT replace(replace(urls.url, 'https://', ''), 'http://', '') AS replaced,
...> visits.visit_duration AS duration
...> FROM visits
...> LEFT JOIN urls
...> ON visits.url = urls.id
...> WHERE urls.url LIKE 'https://%' or urls.url LIKE 'http://%'
...> ), per_domain AS (
...> SELECT CASE
...> WHEN instr(replaced, '/') > 0 THEN substr(replaced, 1, instr(replaced, '/') -1)
...> ELSE replaced
...> END AS domain,
...> duration
...> FROM joined_http_url
...> ), aggregation AS (
...> SELECT domain,
...> sum(duration) AS total
...> FROM per_domain
...> GROUP BY domain
...> )
...> SELECT (total / 3600 / 1000000) || ' hours ' || strftime('%M minutes %S seconds', total / 1000000 / 86400.0) as total_duration,
...> domain
...> FROM aggregation
...> ORDER BY total DESC
...> LIMIT 5
...> ;
total_duration domain
107 hours 44 minutes 31 seconds www.google.com
99 hours 44 minutes 21 seconds docs.python.org
82 hours 56 minutes 20 seconds github.com
64 hours 38 minutes 15 seconds www.rfc-editor.org
64 hours 36 minutes 36 seconds www.ietf.org
アクセス回数について
アクセス回数が多いドメイン順にソートして、上位5件を取得しました。
sqlite> WITH http_url AS ( ...> SELECT replace(replace(urls.url, 'https://', ''), 'http://', '') AS replaced, ...> urls.visit_count ...> FROM urls ...> WHERE urls.url LIKE 'https://%' or urls.url LIKE 'http://%' ...> ), per_domain AS ( ...> SELECT CASE ...> WHEN instr(replaced, '/') > 0 THEN substr(replaced, 1, instr(replaced, '/') -1) ...> ELSE replaced ...> END AS domain, ...> visit_count ...> FROM http_url ...> ), aggregation AS ( ...> SELECT domain, ...> sum(visit_count) AS total ...> FROM per_domain ...> GROUP BY domain ...> ) ...> SELECT total, ...> domain ...> FROM aggregation ...> ORDER BY total DESC ...> LIMIT 5 ...> ; total domain 3240 www.google.com 1340 github.com 1326 docs.google.com 872 twitter.com 395 www.cambly.com
それらしいデータを得ることはできましたが、どうも閲覧時間の方の集計について 主観よりも長い時間になっているように思えます。ページを開きっぱなしにして、別のタブに移動していたとしても、アクセス時間として計上される仕様なのかもしれません。（そのあたりは十分に調べられていません）
what3wordsをDNSで引けるようにした
概要
what3wordsというサービスを使うと、地球上のあらゆる場所を３つの単語で表せます。
例えば自由の女神の松明の場所はtoned.melt.shipで表せます。
https://w3w.co/toned.melt.ship
これを次のように、ドメイン名部分に単語を含ませる形でアクセスできるようにしてみました。
http://toned.melt.ship.point.place
仕組み
上記のpoint.placeドメインにアクセスすると、w3w.coが提供する本来のurlへリダイレクトするようにしています。
IDN対応
what3wordsでは、英単語のみならず日本語の単語でも場所を表すことができます。
例えば、次の単語も自由の女神の場所を表します。
あかり。ふえた。くねくね
ドメイン名は、英単語（ascii文字）のみならず日本語等も表現することができます。
そのため、以下を用いても同様にアクセスすることができます。
完備化の問題をいくつか解いてみたーその2
概要
拙作の完備化ツールをいろいろ使ってみたメモのその2です。 今回は、簡単な状態遷移図に対して用いてみます。 その1はこちらです。115個の完備化の問題を解いています。
やってみた
今回ツールに与える状態遷移図は以下のようにします。 これは、RFC 8555に出てくるとある状態遷移図をアレンジしたものです。
ツールに入力できる形式で表すと以下の通りです。
trnという関数が、状態遷移を示しています。第二引数の状態に於いて、第一引数で示すトリガーが生じると、次の状態に遷移するということを表しています。
$ cat data (VAR x y z) (RULES trn(INIT, INIT) -> PENDING trn(ERROR, PENDING) -> INVALID trn(RECEIVEREQUEST, PENDING) -> READY trn(ERROR, READY) -> INVALID trn(RECEIVEDATA, READY) -> PROCESSING trn(ERROR, PROCESSING) -> INVALID trn(FINISHCREATION, PROCESSING) -> VALID car(cons(x,y)) -> x cdr(cons(x,y)) -> y cdr(NIL) -> NIL apply(NIL, x) -> x apply(x, y) -> apply(cdr(x), trn(car(x),y)) trace(x) -> apply(x, INIT) )
状態遷移図を辿る際に便利な関数traceを定義する為に、trn以外の諸々の関数を定義しています。
traceは、引数に1つのリストをとります。リストは状態遷移の為のトリガーを並べたものです。
traceは、リスト内のトリガー(操作)を全て実行した際の状態を返す関数です。
上記を完備化した書き換え系の下で、次の2つの項が何になるか確認してみたいと思います。 \begin{align} trace([INIT, RECEIVEREQUEST, RECEIVEDATA])\\ trace([INIT, ERROR]) \end{align}
$ wget https://github.com/moratori/clover/releases/download/v2.4.2/clover-linux-x86_64_v2.4.2 && chmod +x clover-linux-x86_64_v2.4.2 $ ./clover-linux-x86_64_v2.4.2 rewrite data 'trace([INIT, RECEIVEREQUEST, RECEIVEDATA])' 'trace([INIT, ERROR])' YES (VAR z x y) (RULES trn(car(NIL),x) -> x apply(cons(y,x),z) -> apply(x,trn(y,z)) apply(cdr(x),trn(car(x),y)) -> apply(x,y) trace(x) -> apply(x,INIT) apply(NIL,x) -> x cdr(NIL) -> NIL cdr(cons(x,y)) -> y car(cons(y,x)) -> y trn(FINISHCREATION,PROCESSING) -> VALID trn(ERROR,PROCESSING) -> INVALID trn(RECEIVEDATA,READY) -> PROCESSING trn(ERROR,READY) -> INVALID trn(RECEIVEREQUEST,PENDING) -> READY trn(ERROR,PENDING) -> INVALID trn(INIT,INIT) -> PENDING ) (COMMENT ERROR < FINISHCREATION < INIT < INVALID < NIL < PENDING < PROCESSING < READY < RECEIVEDATA < RECEIVEREQUEST < VALID < TRN < APPLY < TRACE < CAR < CDR < CONS ) (COMMENT trace([INIT, RECEIVEREQUEST, RECEIVEDATA]) reduced PROCESSING trace([INIT, ERROR]) reduced INVALID )
最後に出力されている通り、 $trace([INIT, RECEIVEREQUEST, RECEIVEDATA])$は、$PROCESSING$となることが分かりました。 また、$trace([INIT, ERROR])$は、$INVALID$となることが分かりました。